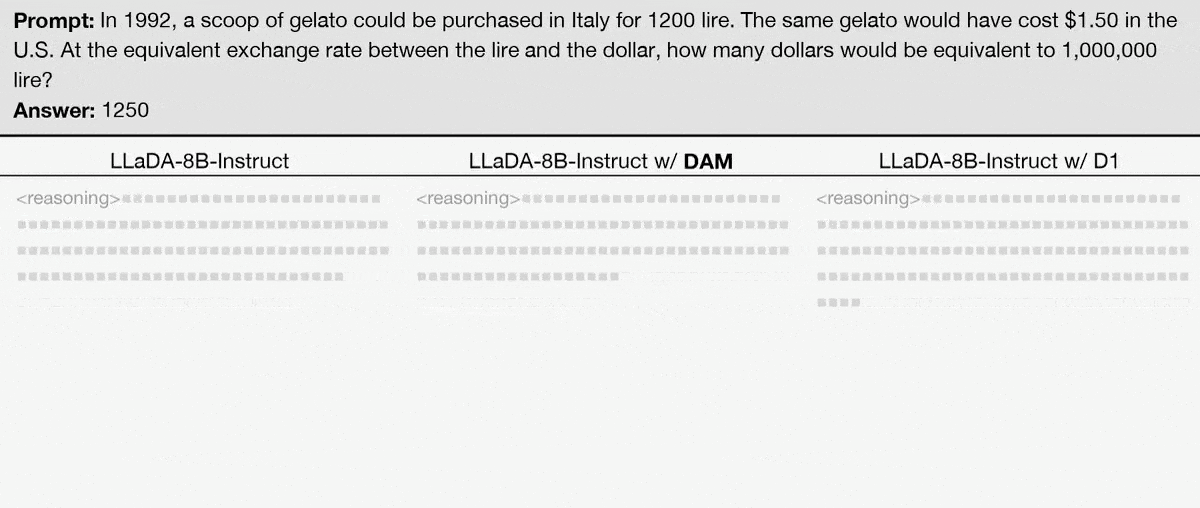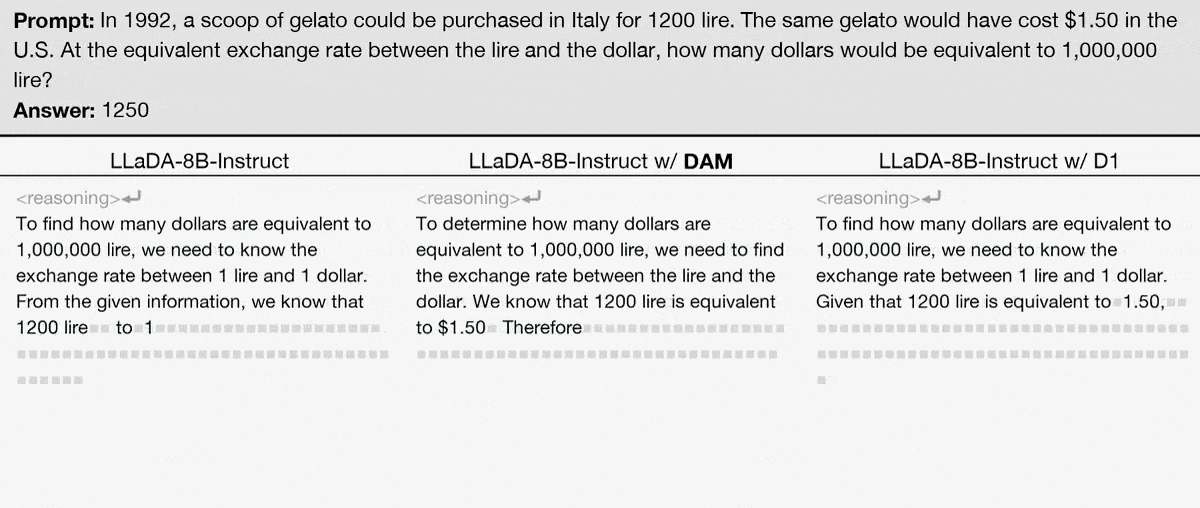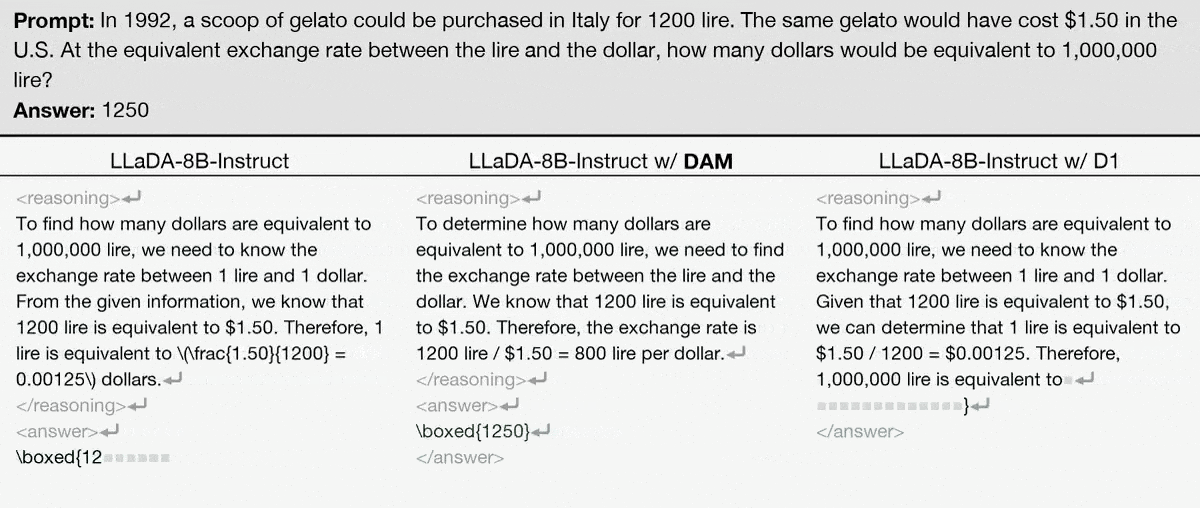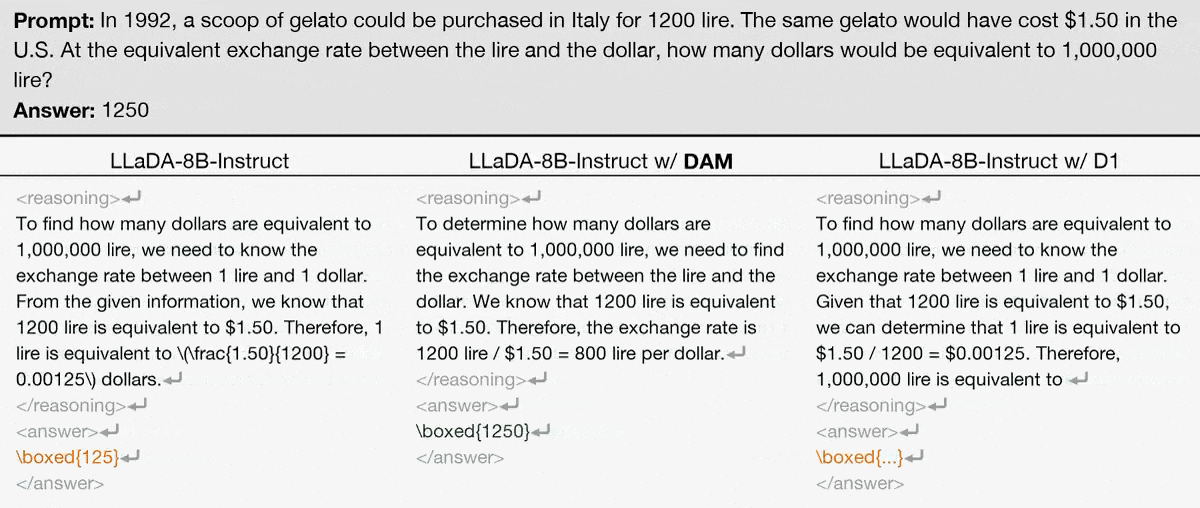
Abstract
Computation methods for solving entropy-regularized reward optimization—a class of problems widely used for fine-tuning generative models—have advanced rapidly. Among those, Adjoint Matching (AM, Domingo-Enrich et al., 2025) has proven highly effective in continuous state spaces with differentiable rewards. Transferring these practical successes to discrete generative modeling, however, remains particularly challenging and largely unexplored, mainly due to the drastic shift in generative model classes to discrete state spaces, which are nowhere differentiable. In this work, we propose Discrete Adjoint Matching (DAM)—a discrete variant of AM for fine-tuning discrete generative models characterized by Continuous-Time Markov Chains, such as diffusion-based large language models. The core of DAM is the introduction of discrete adjoint—an estimator of the optimal solution to the original problem but formulated on discrete domains—from which standard matching frameworks can be applied. This is derived via a purely statistical standpoint, in contrast to the control-theoretic viewpoint in AM, thereby opening up new algorithmic opportunities for general adjoint-based estimators. We showcase DAM's effectiveness on synthetic and mathematical reasoning tasks.