Safety on the Fly:

Constructing Robust Safety Filters via Policy Control Barrier Functions at Runtime

Luzia Knoedler1*, Oswin So2*, Ji Yin3, Mitchell Black4, Zachary Serlin4, Panagiotis Tsiotras3, Javier Alonso-Mora1, Chuchu Fan2
* Both authors contributed equally to this work, 1 Delft University of Technology,, 2 Massachusetts Institute of Technology, 3 Georgia Institute of Technology, 4 MIT Lincoln Labs
Paper Code

Abstract

Control Barrier Functions (CBFs) have proven to be an effective tool for performing safe control synthesis for nonlinear systems. However, guaranteeing safety in the presence of disturbances and input constraints for high relative degree systems is a difficult problem. In this work, we propose the Robust Policy CBF (RPCBF), a practical approach for constructing robust CBF approximations online via the estimation of a value function. We establish conditions under which the approximation qualifies as a valid CBF and demonstrate the effectiveness of the RPCBF-safety filter in simulation on a variety of high relative degree input-constrained systems. Finally, we demonstrate the benefits of our method in compensating for model errors on a hardware quadcopter platform by treating the model errors as disturbances.

Robust Policy CBFs: Constructing robust CBFs from the Policy Value Function

In this work, we leverage the insight that the maximum-over-time constraint function is a CBF for any choice of design policy \(\pi\). The policy value function for a policy \(\pi\) is defined as

\( \displaystyle V_\infty^{h,\pi}(x) \coloneqq \sup_{t \geq 0}\, h(x_t^\pi) \),

where the avoid set \( \mathcal{A} \) is described as the superlevel set of some continuous constraint function \(h\):

\( \displaystyle \mathcal{A} = \{ x \mid h(x) > 0 \} \).

\(V_\infty^{h,\pi}\) contains knowledge about the invariant set, which can be used to render a (potentially unsafe) nominal policy \(\pi_\mathrm{nom}\) safe via a safety filter framework. However, deriving \(V_\infty^{h,\pi}\) over the infinite horizon is computationally intractable. Although an approximation of the policy value function \(V_\infty^{h,\pi}\) can be learned [1] , it requires certifying the neural network as a valid CBF and limits the interpretability. Furthermore, it does not consider uncertainties in the system dynamics. Therefore, we present a practical approximation of Robust Policy CBFs.

We define the robust policy value function equivalent of the above introduced value function as

\( \displaystyle V_\infty^{h,\pi}(x) \coloneqq \sup_{t \geq 0}\, \sup_{d(\cdot)} h(x_t^\pi) \).
Since this formulation is computationally intractable, we propose a practical (finite-time and sampling-based) approximation:
\( \displaystyle V_{T,N}^{h,\pi}(x_0) \coloneqq \max_{i = 1,\ldots,N}\sup_{0 \leq t < T} h(x_t^i) \)

More details can be found in the paper.

Simulation Experiments

To assess the safety improvements brought about by the proposed RPCBF, we integrate it with Shield-MPPI [2] and evaluate the performance on AutoRally.

MPPI

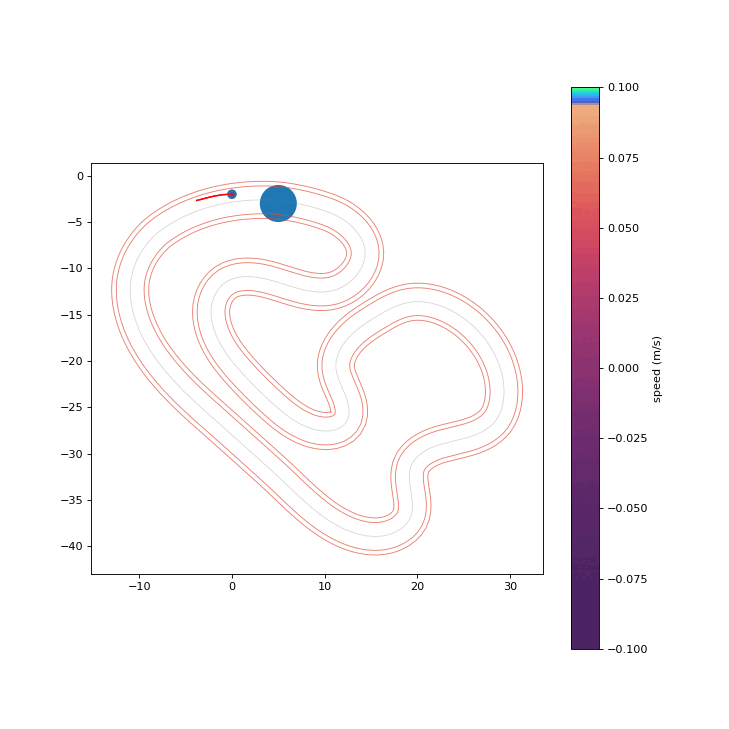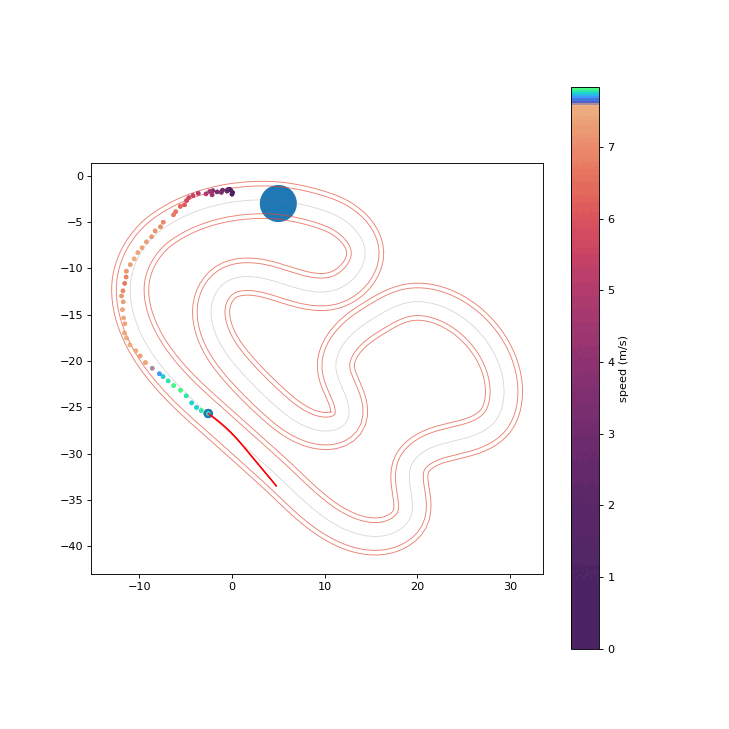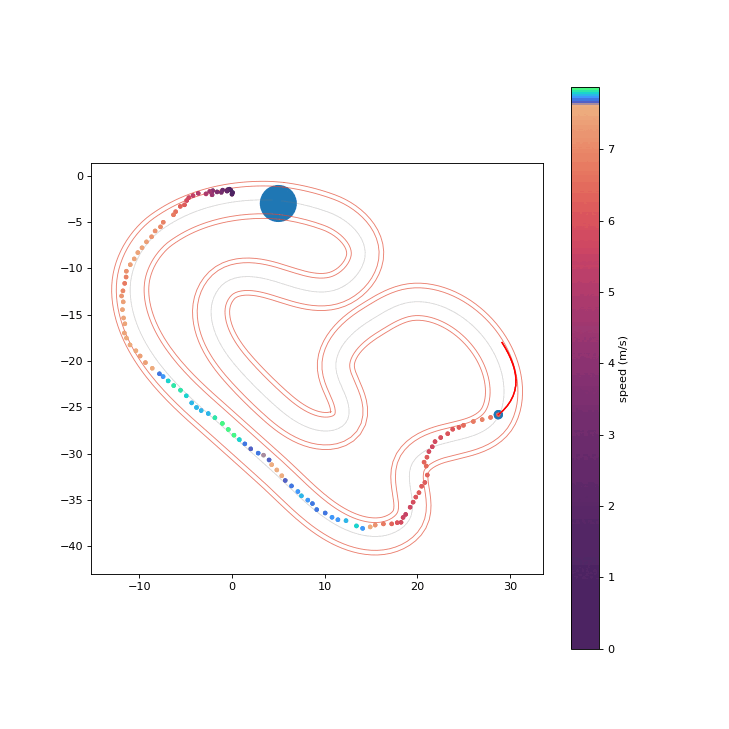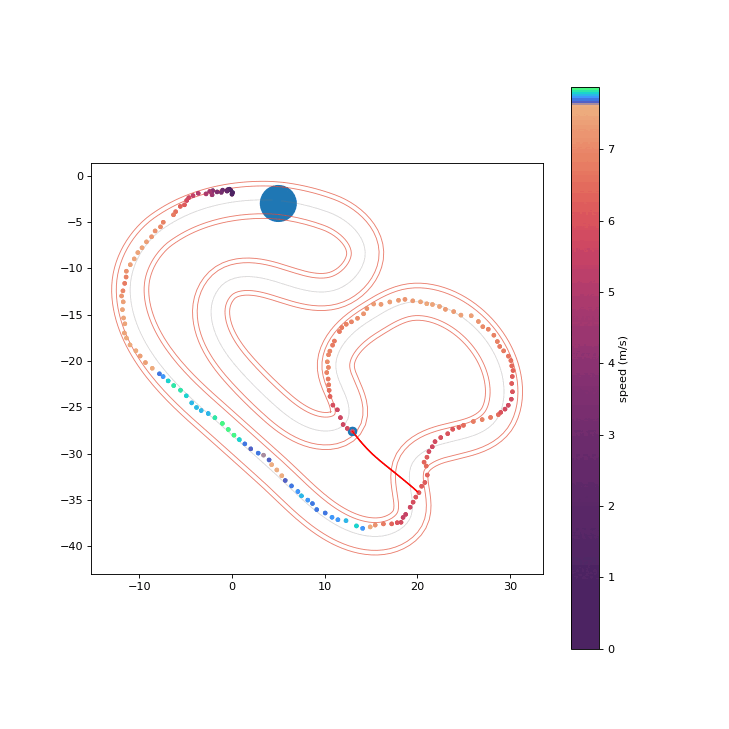
MPPI GIF

Shield-MPPI-RPCBF

Shield-MPPI-RPCBF GIF

Hardware Experiments

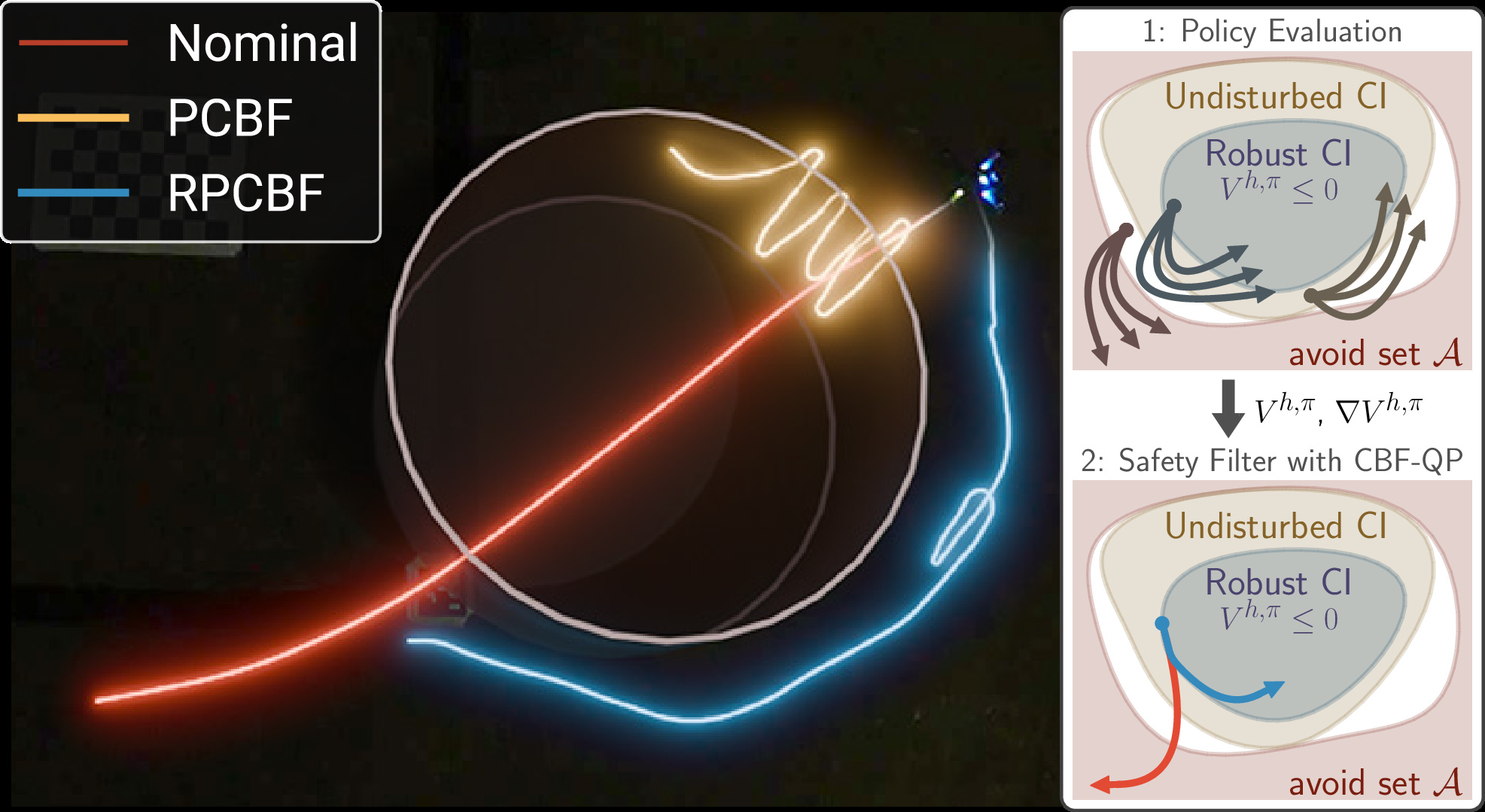
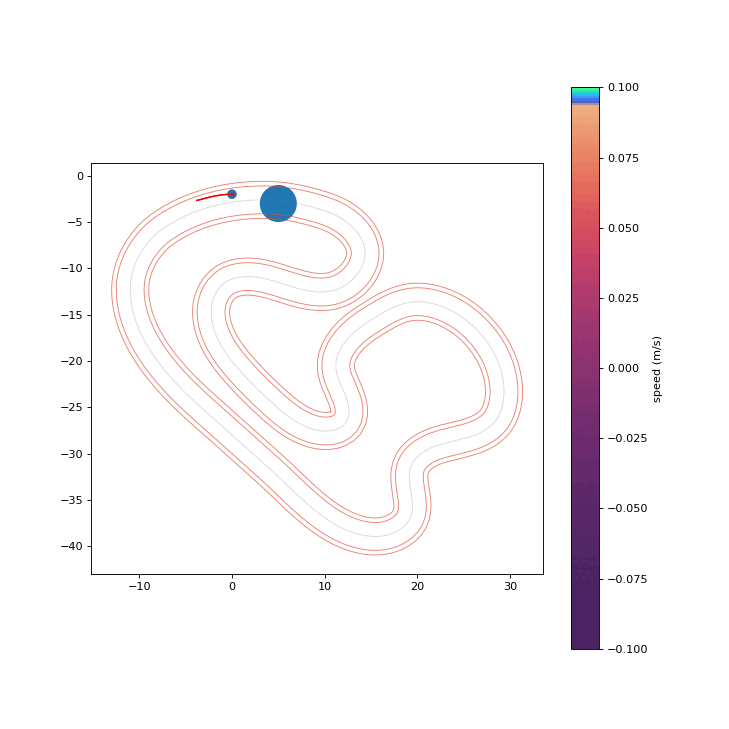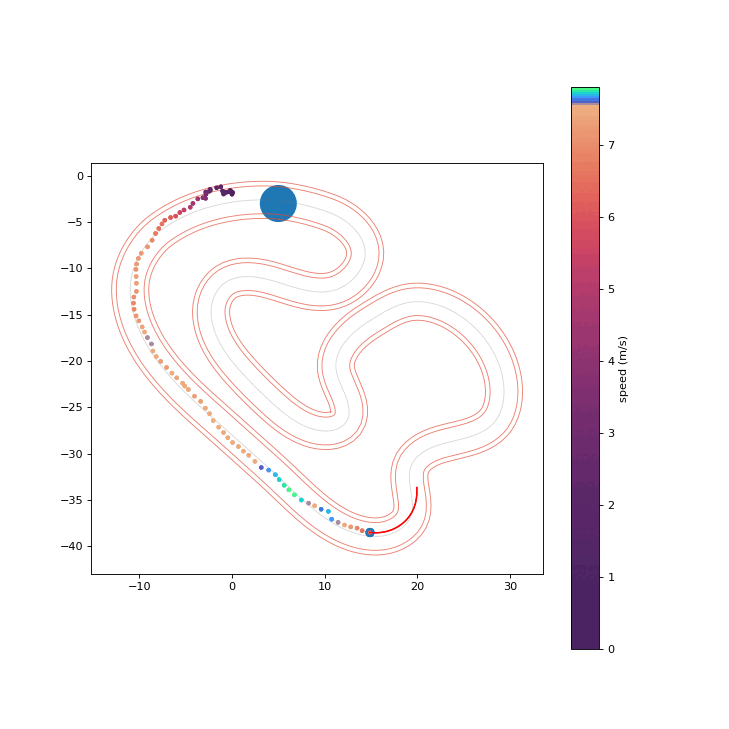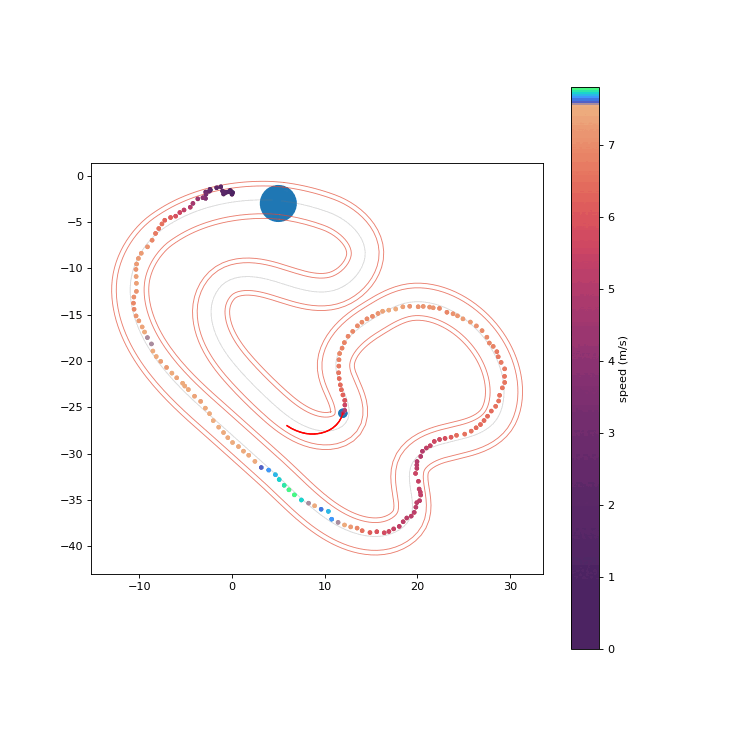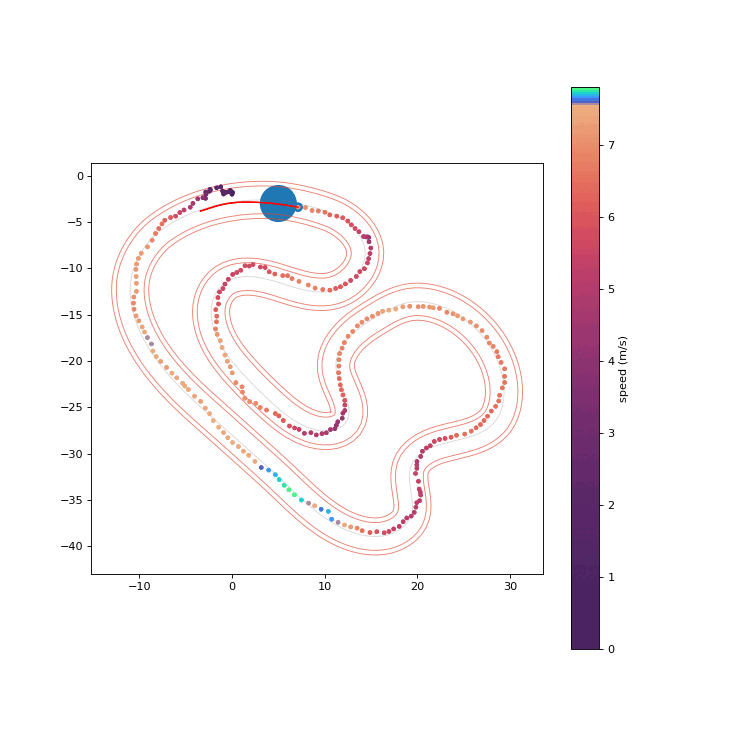
We conduct hardware experiments on the Crazyflie platform to determine whether the proposed RPCBF can be robust to disturbances encountered in the real world. The error between a simple double integrator model and the true dynamics is treated as an acceleration disturbance. We randomly generate an unsafe nominal trajectory which intersects with the cylindrical obstacle and is tracked using the onboard PID controller. The proposed RPCBF safety filter runs at 100 Hz.

PCBF Safety Filter enters Obstacle

RPCBF Safety Filter is safe

-->

Supplementary Video

Related Works

  1. 1. Oswin So, Zachary Serlin, Makai Mann, Jake Gonzales, Kwesi Rutledge, Nicholas Roy, and Chuchu Fan, "How to Train Your Neural Control Barrier Function: Learning Safety Filters for Complex Input-Constrained Systems", IEEE International Conference on Robotics and Automation (ICRA) , 2024
  2. 2. Ji Yin, Charles Dawson, Chuchu Fan, and Panagiotis Tsiotras, "Shield model predictive path integral: A computationally efficient robust MPC method using control barrier functions", IEEE Robotics and Automation Letters , 2023