Solving Minimum-Cost Reach Avoid using Reinforcement Learning

Oswin So1*, Cheng Ge1*, Chuchu Fan1
* Both authors contributed equally to this work 1 Massachusetts Institute of Technology
Paper arXiv OpenReview
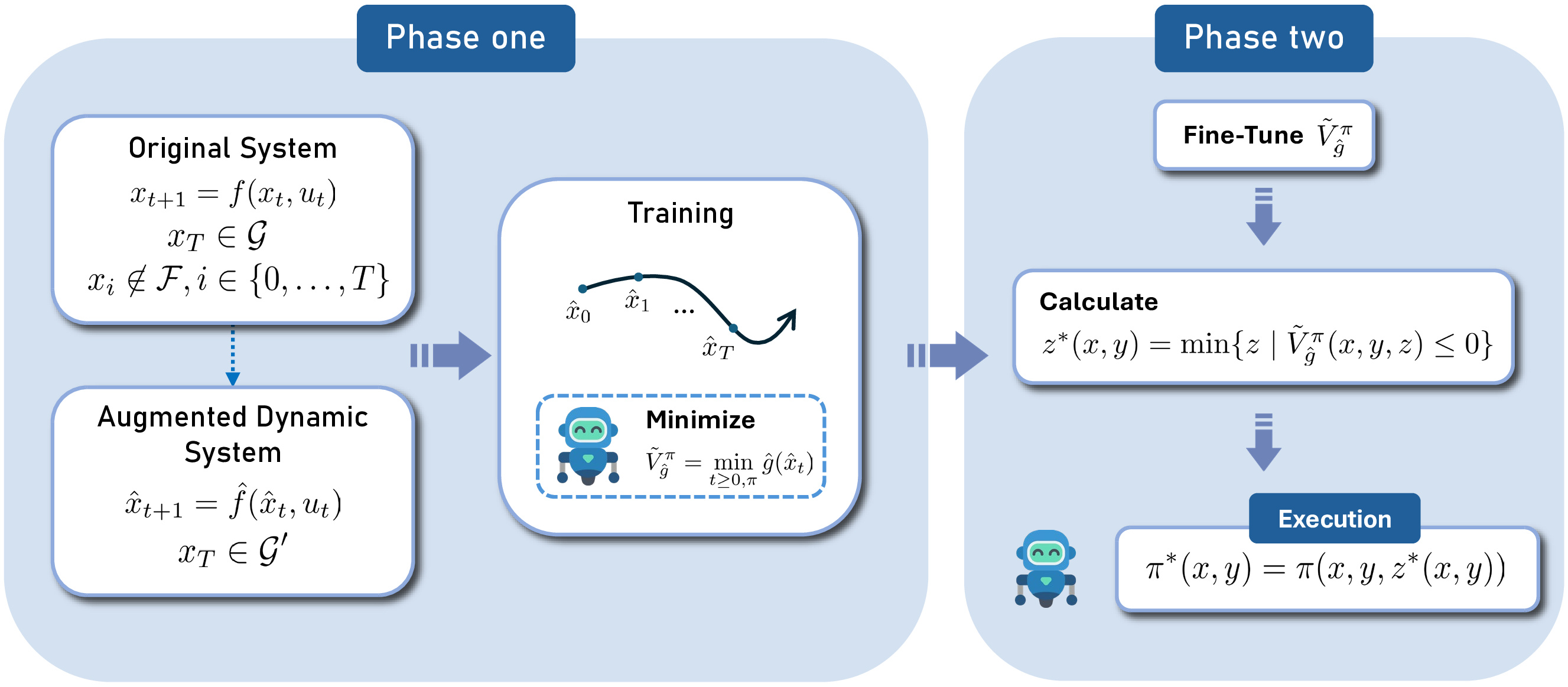
Algorithm

Minimum-Cost Reach Avoid Problem

We tackle the problem of solving minimum-cost reach avoid problems. That is, we wish to minimize the cumulative cost to reach the goal while avoiding collision.

\( \begin{aligned} \min_{\pi, T} \quad &\textcolor{#348ABD}{\sum_{t=0}^{T - 1} l(x_t)}, \\ \text{s.t.} \quad& \textcolor{#FBC15E}{x_T \in \mathcal{G}}, \\ & \textcolor{#E24A33}{x_t \not \in \mathcal{F}}, \quad \forall t \in \{ 0, \dots, T \}, \\ & x_{t+1} = f(x_t, \pi(x_t)) \end{aligned} \)

Unlike normal MDPs, the minimum-cost reach avoid problem has the following differences:

  1. The time horizon \(T\) is a decision variable
  2. Unlike the safety constraint, the goal constraint is only enforced at the terminal timestep T

These differences prevent the straightforward application of existing RL methods to solve this problem.

Experiments

We compare RC-PPO on six minimum-cost reach-avoid environments.

Pendulum
Pendulum
Safety Hopper
Safety Hopper
WindField
WindField
PointGoal
PointGoal
Safety HalfCheetah
Safety HalfCheetah
FixedWing
FixedWing

For each task, we compare the interquartile mean (IQM) of the cumulative and the reach rates of the final converged policies. RC-PPO achieves significantly lower costs while retaining comparable reach rates even when compared to the best baselines that use reward-shaping.

Pendulum
Pendulum
Safety Hopper
Safety Hopper
WindField
WindField
PointGoal
PointGoal
Safety HalfCheetah
Safety HalfCheetah
FixedWing
FixedWing

Abstract

Current reinforcement-learning methods are unable to directly learn policies that solve the minimum cost reach-avoid problem to minimize cumulative costs subject to the constraints of reaching the goal and avoiding unsafe states, as the structure of this new optimization problem is incompatible with current methods. Instead, a surrogate problem is solved where all objectives are combined with a weighted sum. However, this surrogate objective results in suboptimal policies that do not directly minimize the cumulative cost.

In this work, we propose RCPPO, a reinforcement-learning-based method for solving the minimum-cost reach-avoid problem by using connections to Hamilton-Jacobi reachability. Empirical results demonstrate that RCPPO learns policies with comparable goal-reaching rates to while achieving up to 57% lower cumulative costs compared to existing methods on a suite of minimum-cost reach-avoid benchmarks on the Mujoco simulator.